BFS: Shortest Reach in a Graph [HARD]

Consider an undirected graph consisting of  nodes where each node is labeled from  to  and the edge between any two nodes is always of length . We define node  to be the starting position for a BFS.

Given  queries in the form of a graph and some starting node, , perform each query by calculating the shortest distance from starting node  to all the other nodes in the graph. Then print a single line of  space-separated integers listing node 's shortest distance to each of the  other nodes (ordered sequentially by node number); if  is disconnected from a node, print  as the distance to that node.

Input Format

The first line contains an integer, , denoting the number of queries. The subsequent lines describe each query in the following format:

• The first line contains two space-separated integers describing the respective values of  (the number of nodes) and  (the number of edges) in the graph.
• Each line  of the  subsequent lines contains two space-separated integers,  and , describing an edge connecting node  to node .
• The last line contains a single integer, , denoting the index of the starting node.

Constraints

Output Format

For each of the  queries, print a single line of  space-separated integers denoting the shortest distances to each of the  other nodes from starting position . These distances should be listed sequentially by node number (i.e., ), but should not include node . If some node is unreachable from , print  as the distance to that node.

Sample Input

2
4 2
1 2
1 3
1
3 1
2 3
2

Sample Output

6 6 -1
-1 6

Explanation

We perform the following two queries:

1. The given graph can be represented as: 
   
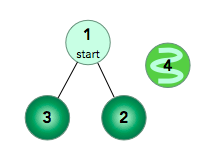
   where our start node, , is node . The shortest distances from  to the other nodes are one edge to node , one edge to node , and an infinite distance to node  (which it's not connected to). We then print node 's distance to nodes , , and  (respectively) as a single line of space-separated integers: 6 6 -1.
2. The given graph can be represented as: 
   
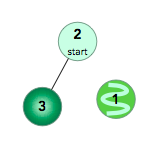
   where our start node, , is node . There is only one edge here, so node  is unreachable from node  and node  has one edge connecting it to node . We then print node 's distance to nodes  and  (respectively) as a single line of space-separated integers: -1 6.

Note: Recall that the actual length of each edge is , and we print  as the distance to any node that's unreachable from .

CODE: Click here