Heaps
A heap is just what it sounds like — a pile of values organized into a binary tree-like structure adhering to some ordering property. When we add elements to a heap, we fill this tree-like structure from left to right, level by level. This makes heaps really easy to implement in an array, where the value for some index 's left child is located at index and the value for its right child is at index (using zero-indexing). Here are the two most fundamental heap operations:
- add: Insert an element into the heap. You may also see this referred to as push.
- poll: Retrieve and remove the root element of the heap. You may also see this referred to as pop.
Max Heap
This type heap orders the maximum value at the root.
When we add the values to a Max heap, it looks like this:

When we poll the same Max heap until it's empty, it looks like this: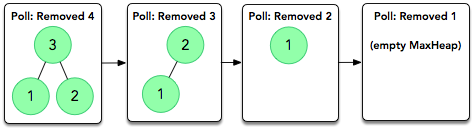

Min Heap
This type of heap orders the minimum value at the root.
When we add the values to a Min heap, it looks like this:

When we poll the same Min heap until it's empty, it looks like this:

Example
EXAMPLE
The Java code below implements, fills, and empties a Min Heap and a Max Heap.
1
import java.util.*;
2
3
/** Heap of ints **/
4
abstract class Heap {
5
/** Current array length **/
6
protected int capacity;
7
/** Current number of elements in Heap **/
8
protected int size;
9
/** Array of Heap elements **/
10
protected int[] items;
11
12
public Heap() {
13
this.capacity = 10;
14
this.size = 0;
15
this.items = new int[capacity];
16
}
17
18
/** @param parentIndex The index of the parent element.
19
@return The index of the left child.
20
**/
21
public int getLeftChildIndex(int parentIndex) {
22
return 2 * parentIndex + 1;
23
}
24
25
/** @param parentIndex The index of the parent element.
26
@return The index of the right child.
27
**/
28
public int getRightChildIndex(int parentIndex) {
29
return 2 * parentIndex + 2;
30
}
31
32
/** @param childIndex The index of the child element.
33
@return The index of the parent element.
34
**/
35
public int getParentIndex(int childIndex) {
36
return (childIndex - 1) / 2;
37
}
38
39
/** @param index The index of the element you are checking.
40
@return true if the Heap contains enough elements to fill the left child index,
41
false otherwise.
42
**/
43
public boolean hasLeftChild(int index) {
44
return getLeftChildIndex(index) < size;
45
}
46
47
/** @param index The index of the element you are checking.
48
@return true if the Heap contains enough elements to fill the right child index,
49
false otherwise.
50
**/
51
public boolean hasRightChild(int index) {
52
return getRightChildIndex(index) < size;
53
}
54
55
/** @param index The index of the element you are checking.
56
@return true if the calculated parent index exists within array bounds
57
false otherwise.
58
**/
59
public boolean hasParent(int index) {
60
return getParentIndex(index) >= 0;
61
}
62
63
/** @param index The index of the element whose child you want.
64
@return the value in the left child.
65
**/
66
public int leftChild(int index) {
67
return items[getLeftChildIndex(index)];
68
}
69
70
/** @param index The index of the element whose child you want.
71
@return the value in the right child.
72
**/
73
public int rightChild(int index) {
74
return items[getRightChildIndex(index)];
75
}
76
77
/** @param index The index of the element you are checking.
78
@return the value in the parent element.
79
**/
80
public int parent(int index) {
81
return items[getParentIndex(index)];
82
}
83
84
/** @param indexOne The first index for the pair of elements being swapped.
85
@param indexTwo The second index for the pair of elements being swapped.
86
**/
87
public void swap(int indexOne, int indexTwo) {
88
int temp = items[indexOne];
89
items[indexOne] = items[indexTwo];
90
items[indexTwo] = temp;
91
}
92
93
/** Doubles underlying array if capacity is reached. **/
94
public void ensureCapacity() {
95
if(size == capacity) {
96
capacity = capacity << 1;
97
items = Arrays.copyOf(items, capacity);
98
}
99
}
100
101
/** @throws IllegalStateException if Heap is empty.
102
@return The value at the top of the Heap.
103
**/
104
public int peek() {
105
isEmpty("peek");
106
107
return items[0];
108
}
109
110
/** @throws IllegalStateException if Heap is empty. **/
111
public void isEmpty(String methodName) {
112
if(size == 0) {
113
throw new IllegalStateException(
114
"You cannot perform '" + methodName + "' on an empty Heap."
115
);
116
}
117
}
118
119
/** Extracts root element from Heap.
120
@throws IllegalStateException if Heap is empty.
121
**/
122
public int poll() {
123
// Throws an exception if empty.
124
isEmpty("poll");
125
126
// Else, not empty
127
int item = items[0];
128
items[0] = items[size - 1];
129
size--;
130
heapifyDown();
131
return item;
132
}
133
134
/** @param item The value to be inserted into the Heap. **/
135
public void add(int item) {
136
// Resize underlying array if it's not large enough for insertion
137
ensureCapacity();
138
139
// Insert value at the next open location in heap
140
items[size] = item;
141
size++;
142
143
// Correct order property
144
heapifyUp();
145
}
146
147
/** Swap values down the Heap. **/
148
public abstract void heapifyDown();
149
150
/** Swap values up the Heap. **/
151
public abstract void heapifyUp();
152
}
153
154
class MaxHeap extends Heap {
155
156
public void heapifyDown() {
157
int index = 0;
158
while(hasLeftChild(index)) {
159
int smallerChildIndex = getLeftChildIndex(index);
160
161
if( hasRightChild(index)
162
&& rightChild(index) > leftChild(index)
163
) {
164
smallerChildIndex = getRightChildIndex(index);
165
}
166
167
if(items[index] > items[smallerChildIndex]) {
168
break;
169
}
170
else {
171
swap(index, smallerChildIndex);
172
}
173
index = smallerChildIndex;
174
}
175
}
176
177
public void heapifyUp() {
178
int index = size - 1;
179
180
while( hasParent(index)
181
&& parent(index) < items[index]
182
) {
183
swap(getParentIndex(index), index);
184
index = getParentIndex(index);
185
}
186
}
187
}
188
189
class MinHeap extends Heap {
190
191
public void heapifyDown() {
192
int index = 0;
193
while(hasLeftChild(index)) {
194
int smallerChildIndex = getLeftChildIndex(index);
195
196
if( hasRightChild(index)
197
&& rightChild(index) < leftChild(index)
198
) {
199
smallerChildIndex = getRightChildIndex(index);
200
}
201
202
if(items[index] < items[smallerChildIndex]) {
203
break;
204
}
205
else {
206
swap(index, smallerChildIndex);
207
}
208
index = smallerChildIndex;
209
}
210
}
211
212
public void heapifyUp() {
213
int index = size - 1;
214
215
while( hasParent(index)
216
&& parent(index) > items[index]
217
) {
218
swap(getParentIndex(index), index);
219
index = getParentIndex(index);
220
}
221
}
222
223
public static void main(String[] args) {
224
Scanner scanner = new Scanner(System.in);
225
int range = scanner.nextInt();
226
scanner.close();
227
228
// Insert random values into heaps:
229
Heap minHeap = new MinHeap();
230
Heap maxHeap = new MaxHeap();
231
System.out.println("Insert Number Sequence:");
232
for(int i = 0; i < range; i++) {
233
int value = (int) (Math.random() * 100);
234
minHeap.add(value);
235
maxHeap.add(value);
236
System.out.print(+ value + " ");
237
}
238
239
// Remove values from heaps:
240
System.out.println("\n\nPoll Values:\n------------\nMinHeap MaxHeap");
241
for(int i = 0; i < range; i++) {
242
System.out.format(" %-12d", minHeap.poll());
243
System.out.format("%-6d\n", maxHeap.poll());
244
}
245
try {
246
minHeap.peek();
247
}
248
catch(IllegalStateException e) {
249
System.out.println(e.getMessage());
250
}
251
try {
252
maxHeap.poll();
253
}
254
catch(IllegalStateException e) {
255
System.out.println(e.getMessage());
256
}
257
}
258
}
- Get link
- X
- Other Apps
Labels
hackerrank heaps
Labels:
hackerrank
heaps
- Get link
- X
- Other Apps
Comments
Post a Comment