N Queen Problem [Hard]

Company:
Visa, Twitter, MAQ-Software, Amdocs, Amazon, Accolite

Question:
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other. Given an integer n, print all distinct solutions to the n-queens puzzle. Each solution contains distinct board configurations of the n-queens’ placement, where the solutions are a permutation of [1,2,3..n] in increasing order, here the number in the ith place denotes that the ith-column queen is placed in the row with that number. For eg below figure represents a chessboard [3 1 4 2].



Input:
The first line of input contains an integer T denoting the no of test cases. Then T test cases follow. Each test case contains an integer n denoting the size of the chessboard.

Output:
For each test case, output your solutions on one line where each solution is enclosed in square brackets '[', ']' separated by a space . The solutions are permutations of {1, 2, 3 …, n} in increasing order where the number in the ith place denotes the ith-column queen is placed in the row with that number, if no solution exists print -1.
Constraints:
1<=T<=10
1<=n<=10

Example:
Input
2
1
4
Output:
[1 ]
[2 4 1 3 ] [3 1 4 2 ]

Explanation:
Note: I saw this on a site and thought to add it here. Kudos to the author.
Find all valid configuration of N Queens puzzle. To understand this better, let us look into an example – 4 queen’s problem. I am taking the 4 queens problem as there are no solutions for 2 and 3 queen’s problem and 1 queen problem is trivial one. For this, we are given 4 x 4 chessboard and we need to place 4 queens in non-attacking places on this board. Following are the only two configurations which exist for this 4 queen’s problem.

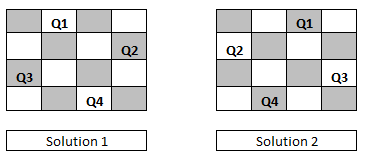4 Queen Solutions

Backtracking Algorithm:
Before we get on to the actual solution, let us look into the backtracking algorithm.  Backtracking is similar to the brute force approach where it tries all of the solutions but the only difference is that it eliminates/avoids the partial candidate solutions as soon as it finds that that path cannot lead to a solution.

To understand this further, let us look into the following tree. By the way, this is called Trie or prefix tree and let us not worry about these in this post.

Backtracking Algorithm

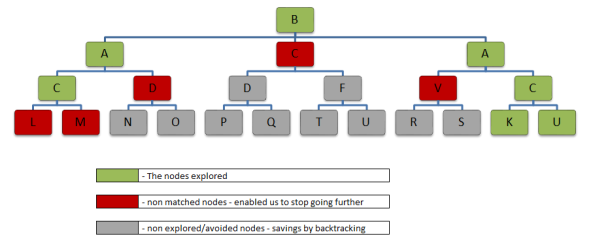Backtracking Algorithm

In the above mentioned tree, what path leads to the word “BACK” (first 4 letters of backtracking)?
One of the simple way, I can think is as follows.

Start at the root node ‘B’. Does this match with the 1st letter of the word BACK? YES
Then check the 1st child node A – does this match 2nd letter of the word BACK? YES
Then check the 1st child C – does this match 3rd letter of the word BACK? YES
Check the 1st child L – does this match 4th letter of the word BACK? NO
Check the 2nd child M – does this match 4th letter of the word BACK? NO
Check the 2nd child D – does this match 3rd letter of the word BACK? NO
Check the 2nd child node C – does this match 2nd letter of the word BACK? NO
Check the 3rd child node A – does this match 2nd letter of the word BACK? YES
Check the 1st child V – does this match 3rd letter of word BACK? NO
Check the 2nd child C – does this match 3rd letter of the work BACK? YES
Check the 1st child K – does this match 4th letter of the work BACK? YES
Following are the observations based on the above steps,

Every time when we hit NO, we went back to parent of that node and checked other child nodes/paths – this is back tracking
Avoided all of the sub paths for the node whenever we hit non match (NO). This enabled us to avoid unnecessary paths exploration(2nd node C – at level 2 and others)

Algorithm:

Take a sub problem.
       For each of the possible candidates for this sub problem
           If this can lead to the solution, then recursively
           call this for next sub problem
           If not, then skip this possibility and investigate next candidate.
If all of the sub problems are solved,
      Then we found a solution otherwise, no solution

Solution:

As we now have the understanding of the backtracking algorithm let us see how that applies to our N Queens problem.

We can divide this problem into a sub problem of placing single queen on the chess board
To identify if this leads to a solution, we can check and see does any of the already placed queens attack this position. If yes, then go to next column. If no, then place this queen and move on to next queen
To illustrate this further,

Did we place all of the queens?
YES, we found the successful configuration. Print it.
NO, Take the queen
For each column from 1 to N
Does this column is safe – YES, then iterate this process for next queens – call this method recursively
NO – continue with next column
In Java
We can always represent the queen’s placement in an N x N array but let us use an array with N elements which stores the column positions of each array. For example, if A[2] = 5, it means the 2nd queen is placed on column 5. This way we can save the memory and also it is easy to find if a cell in the board is safe to place or not.

To find if the cell is safe of not, we need to look into two aspects.

Does any of the previously placed queen is in the same column?
This can easily be checked using the above noted array representation. Iterate through above noted array and see does any of the value matches the column we are trying to place current queen. By the way we need not check for the row as we construct the solution row by row and there will not be any queens placed in those.

Does any of the previously placed queen is in diagonal?
This is a bit tricky. The way can find is, iterate through each of the previously placed queen positions and check the absolute differences between the column and row value. If they are same, then they are in attacking position. Let us take an example here. Assume that we already placed first queen in (2, 2) – 2nd queen is placed in 2nd column. If we look at the diagonal cells (1,1), (1,3), (3,1), (3.3), we can observe that,


|r1-r2| == |c1-c2| is hold good.


Code:
import java.util.*;
import java.lang.*;
import java.io.*;

class GFG {
public static void main (String[] args) {
//code
Scanner sc = new Scanner (System.in);
int m = sc.nextInt();
for (int k=0;k<m;k++){
   int n = sc.nextInt();
   int [] board = new int[n];
   PlaceQueen(0,board);
}
}
public static void PlaceQueen(int Qi, int [] board){
   int n = board.length;
   if (Qi==n){
       System.out.println(Arrays.toString(board));
   } else
   for (int col=1;col<=n;col++){
       if(isSafePlace(Qi,col,board)){
           board[Qi]=col;
           PlaceQueen(Qi+1,board);
           board[Qi]=-1;
       }
   }
}
public static boolean isSafePlace(int Qi,int col,int[]board){
   for(int i=0;i<Qi;i++){
       if(board[i]==col)
       return false;
       if(Math.abs(i-Qi)==Math.abs(board[i]-col)){
           return false;
       }
   }
   return true;
}

}